Andy's blog

Latent Dirichlet allocation

Latent Dirichlet allocation, or LDA for short, is the topic of my first blog post. Let me be honest with you, I only learned it a few days ago. “Then what gives you the authority to explain it to other people?!” – you might be wondering. Nothing. It’s my blog, I can do what I want. I just got my bachelor’s degree in Mathematics & Computer Science, so you should be reading this with a grain of salt. Anyway, lets dive in.

History and motivation

LDA was discovered by two groups of scientists independently in the early 2000s. Both papers have over 20,000 citations making them one of the most cited ones in the field of Machine Learning. LDA is a topic model, meaning that it is mostly used to infer things about topics of certain documents. In a nutshell, what LDA does is, it takes a set of sentences like “The quick brown fox jumps over the lazy dog” and spits out something like “this sentence is 70% about animals, 10% about foxes and 20% about dogs.”

However, applications are not just limited to words and documents. A cool one is grouping individuals in a population by their genetic profile. In fact, one of the two papers mentioned above is called “Inference of population structure using multilocus genotype data” and does something along those lines..?

Anyway, in the research of topic modelling, there’s four main words that people use: a corpus, a document, a word and a topic. A corpus consists of many documents, a document consists of many words and each document might be about a topic or several. In this sense:

After statistical inference, the applications of LDA include:

and many more that I am probably unaware of.

Wikipedia says that latent Dirichlet allocation is a generative statistical model. What do all these fancy words mean?

Well, latent here refers to something that is unobserved. Something we believe that exists there and matters but is not explicitly shown or written in the data. In our case, when we’re dealing with, say Wikipedia articles, it could be the topic. You might say – “Wait, Wikipedia articles have a title, doesn’t that sort of give us an explicitly written topic?”. I agree, it sort of does. But Wikipedia articles have very different and specific titles, like “Battle of Grunwald” or “Rice’s theorem”, and our goal is to group them together into clusters that have much more general topics, like “History” or “Mathematics”.

Dirichlet refers to Johann Peter Gustav Lejeune Dirichlet, who was a German mathematician. Fun fact – as he comes from the Belgium town of Richelet, the origins of his name could be explained by “Le jeune de Richelet” meaning “Young from Richelet”. Read more about him here! Anyway, since he was a sick mathematician a lot of theorems and objects in mathematics are named after him. LDA uses the Dirichlet distribution, which we’ll talk about later.

Statistical models and inference

What does generative statistical model mean? Statistical model is kind of obvious because we’re somehow going to model the world that we’re observing but it’s also unclear as we don’t know what approach to modelling the world the statisticians take. When a statistician looks at some data, say the numbers

1, 4, 2, 6, 2, 1, 1, 2, 5, 5

generally the question they ask is something along the lines of

I wonder how these numbers are generated?

In fact, generative means that they’re interested in exactly this question. The answer could be

I bet Andy just rolls a fair 6-sided die

and that would be correct. Or, if they look at the numbers

2, 2, 1, 1, 6, 6, 3, 3, 6, 6

they could say

I bet Andy rolls a fair 6-sided die and then writes the number twice

That would also be correct.

One of the key ingredients that statisticians use for coming up with such answers are statistical models. A statistical model is essentially a set of assumptions about how the data can be generated. For instance, a statistical model could be:

I assume that the way Andy generates all of his numbers is by rolling a one 6-sided die, but it’s not necessarily a fair one.

After looking at some of the numbers I have generated, you could then say:

I bet Andy generates his numbers with a 6-sided die where the even numbers show up 75% of the time and odds 25%

This is called statistical inference.

Let’s do a simple exercise. Suppose that I generate a sequence of 0s and 1s, like

0101100011000

If you wanted to do statistical analysis on these numbers, you could have a model that says

I assume that Andy flips a coin that shows 1 with probability p and 0 with probability 1 – p, where p is in [0, 1]

How could we do statistical inference on this? Well, let’s just guess a value of p, say 1/3. Under the assumption that it is the actual parameter of my coin, what is the probability of observing the sequence above? Well, it’s 1/3 for each of the 1s that I flip and 2/3 for each 0. So, the probability is

This is called the likelihood. For each value of the parameter p, I can calculate the likelihood of observing the sequence we have and then take the one that maximizes it. This is called maximum likelihood estimation and is a standard statistical inference technique. In this simple case it coincides with the proportion of ones in the sequence, which is 5/13 and gives a likelihood of around 0.017%.

There are various ways of doing statistical inference, but they fall into different schools of thought and it gets much more complicated philosophically, so let’s leave that for the future.

Having decrypted all this, it seems that LDA should be some set of assumptions that describe how the text in our documents is randomly generated, i.e. the generative process of the corpus. That’s exactly what it is. However, that’s not the only thing that the paper talks about. When someone presents a new model, they have to show why it’s useful. They usually present how statistical inference on that model could be done and then run experiments on different datasets with different applications, to compare results. However, I am only going to go through the actual model definition itself.

So, what could the assumptions be? Let’s start with a simple one.

Unigram model

It could be the case that all the words in Wikipedia articles are generated randomly and independently from each other and the articles. What this assumption basically says is that every time a person sits down to write a Wikipedia article, they repeatedly roll an N-sided die (where N is the number of words in the English dictionary) with words written on the sides and pick the word that gets rolled. A couple of important details:

This is called a unigram model. Working under this model and having access to all Wikipedia articles, how could we statistically infer what die is used across Wikipedia? Remember maximum likelihood estimation? In this simple case, it coincides with the proportions as well. So, if there are 1000 words in Wikipedia and 432 of them are “hello”, then our guess is that the side of the die corresponding to the word “hello” gets rolled 43.2% of the time.

What are the problems with this model? Well, there’s lots. One of them is independence of words. Clearly, if I read the word “dinosaur” in the beginning of a Wikipedia article then the chances of reading the word “cosmetics” sometime later decreases significantly. It means that even though the words across the articles might still be independent the words in the same article aren’t.

Mixture of unigrams

One way to incorporate this into our model is to drop the assumption that there’s only one die. Instead, we assume that there’s some fixed number (that we know), say 20, of topics. Each of the topics has a unique die attached to it with different proportions for all words, we’ll call them topic-word dice. For example, the die representing “History” could be one that has a much higher chance of rolling the word “battle” than the rest of the dice. In this case, our model assumes that every time someone writes an article in Wikipedia, they

  1. Roll a separate 20-sided die (this is not one of the 20) ONCE that decides the single topic of their article
  2. Take the topic-word die for that topic and roll it repeatedly, writing the words corresponding to the numbers rolled.

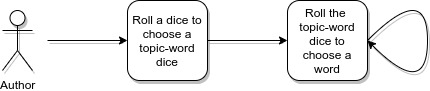
Can you see how if we had just one topic, this model would be exactly the same as Unigram model? For that reason this model is called a mixture of unigrams. Notice how here we assume that there is a topic chosen randomly and how it is not explicitly written anywhere in the articles. This is exactly what the word latent means in the LDA.

Also notice that under this model, after observing some documents, if we wanted to do any sort of statistical inference, we would have to somehow guess the proportions of the 21 dice. How could we do that? That’s quite complicated and I won’t touch it here, but there are algorithms that can approximate the answer.

The weakness of mixture of unigrams is that it doesn’t allow one document to have several topics. Consider the proportions of words in different Wikipedia articles. What do we expect them to be? Well, for each document, we roll a die deciding the topic. The topic in turn decides the proportions according to which we’re going to be generating our words. So, there can only be just 20 different sets of proportions in our corpus! This becomes an issue when the corpus becomes big and the documents have some overlaps.

Probabilistic latent semantic indexing

One model that solves exactly this issue is probabilistic latent semantic indexing or pLSI for short. It essentially assumes that:

Then when someone sits down to write a document, they:

  1. REPEATEDLY FOR EACH WORD roll the unique document-topic die to choose a topic
  2. Take the corresponding topic-word die and roll it to choose the next word

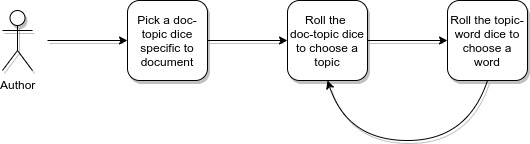
Great, now each document can have its own unique proportions for topics.

So why is pLSI bad, can we not just stop here? Well, among other things, pLSI can be very prone to overfitting, a concept that I want to leave out for now. It essentially means that the model doesn’t generalize well, i.e. we would struggle to make confident predictions on documents that look even slightly different from the ones we have now. This happens because the unique document-topic dice altogether have lots of parameters and so they can fit quite complex functions.

To solve this problem, finally, LDA steps in. If you thought that the procedures above were ridiculous ways of writing Wikipedia articles, strap in.

Random Variables and Dirichlet distribution

Remember how we were generating random numbers with dice? Well, that was fun, but also quite limiting. Specifically, every time we rolled a single fixed die it gave us only one number and that number came from a finite set of possibilities. What if we wanted a roll of a die give us several numbers? What if we wanted those numbers to be anywhere between 0 and 1?

In cases like this what mathematicians like to do is to just imagine non-existing things (sort of). In probability theory, the main object of interest is a random variable. It’s like a die, but way more expressive. It’s possible to variously play with these random variables to construct new ones. For example, suppose we defined a random variable X to be a fair coin flip (like a 2-sided die), i.e. 50% of the time X has the value of 0 (for tails) and 50% of the time it has a value of 1 (for heads). We can define a new random variable Y in terms of X now. For instance, Y = 3 * X + 1. Then 50% of the time Y is 1, and 50% of the time it’s 4. Doesn’t look useful right?

Well we can also do some more complicated things. For instance, we can try and randomly generate numbers from 0 to 1. Firstly, we cut the interval [0, 1] in half to get intervals [0, ½] and [½, 1]. Then we flip a coin and keep [0, ½] if it was 0, and [½, 1] if it was 1. We do this repeatedly with the intervals that we are left with and on every step the length of our interval halves. It means, that if we do this infinitely many times the length of the interval is going to converge to zero, containing just one number, which we can take as our random number. Cool, huh? Also, if I wanted a single random variable to give me several numbers, I could now do something like this Z = (X, Y).

Let’s think about something crazier. What if I wanted to generate a random 6-sided die? What properties should my random variable have? Well, mathematically a 6-sided die is described by 6 numbers – the proportions of each of the sides. They are all positive real numbers that sum up to 1. Are there any random variables that could give me such 6 numbers? Yes, that is exactly what Dirichlet distribution describes.

Dirichlet distribution describes random variables which can generate other random variables. In our case, we will be generating dice for choosing topics. Dirichlet distribution will have a parameter for each topic. Depending on them, Dirichlet distribution could give us maybe only those dice that almost always choose one specific topic. Or maybe those dice that choose topics very uniformly. This will be inferred by LDA.

Latent Dirichlet allocation

So finally, how do the authors write Wikipedia articles in the world of the LDA model? Well, LDA is almost like pLSI except that the dice for each document are random and not fixed. Specifically, before writing an article, each author randomly generates a new 20-sided dice according to the Dirichlet distribution. The rest is all the same. To write each word the author rolls this die to select a topic and another one to select a word. That’s it. This is the latent Dirichlet allocation model in its simplest form.

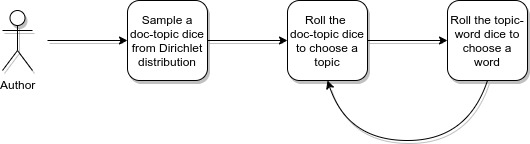
You could be a little bit disappointed by the simplicity of this model and say “wait, how can it be good enough for applications? It doesn’t capture any complexity of how people actually generate content, what the syntax of the language is, etc.?” Well, that’s true. But think about how you would assign topics to Wikipedia articles yourself? Would you read the whole article and pay much attention to how the language is structured? Or would you just skim through the page looking for some hot words? Probably the latter, right? Now, I’m not trying to make some sort of connection between the human brain and LDA. What I’m trying to say is that our brain is pretty damn good at doing these tasks. Every time you go outside and look at grass, you don’t pay attention to every single stem of grass to realize that you’re outside, do you? If you did, you would probably go nuts. And the reason you don’t is because it doesn’t matter. Over the years of evolution, the mammal brain has learned to only pay attention to the things that carry the most useful information to them. (I’m not in any way an evolutionary biologist, so what I just said might be a load of bollocks). So probably, just looking at what words appear in the article give quite a lot of information about the topic. And LDA does exactly that. It models the distributions of topics in documents and the words that they generate.

So, what can we do with this model now?

Well, imagine we’re given a corpus of documents and we’re somehow interested in the underlying topics. Then the most promising objects for us to know are the document-topic and topic-word dice that were used to generate these documents, right? We could use some statistical inference techniques to determine them. Again, the way it’s done is quite complicated and I will leave this aside. The interested reader should refer to Gibbs sampling and expectation-maximization algorithms.

If now we want to, say, cluster the documents into folders by topic, we should somehow determine how similar the topics of documents are. A good way to do this is to just look at the document-topic dice. If those dice have similar proportions then probably the documents have similar topics as well, right? But how do we measure similarity of two dice? One way is to use Kullback-Leibler divergence – a function that quantifies how similar two random variables, or in our case document-topic dice, are. Using KL divergence, we can compute a similarity matrix between documents and then “just apply a standard clustering algorithm.”

And this is how LDA works.:) Every time you look at how Google News has sorted it’s articles, or Netflix is recommending movies, you’ll now know that it’s not a magical box loaded with wisdom, but merely a statistical model that captures some of the most important topic properties of these objects.

Alright, dudes, dudettes & non-binary friends. I’m putting a full stop for today. Congratulations for making it to the end, below is a virtual high five. I hope you had a nice read. If you want me to explain something else (maybe you’re unsatisfied with “just apply a standard clustering algorithm” and want me to elaborate?) let me know.

Written on October 3rd , 2019 by Andy
Feel free to share!

comments powered by Disqus